SEMESTER PROJECTLunar Response to Gravtiational Waves
Semester Project
January 2024 - June 2024
Supervisors
- Prof. Dr. Philippe Jetzer, University of Zurich
- Prof. Dr. Gian Michele Graf, ETH Zürich
Physics Institute – Gravitation and Astrophysics Group
University of Zurich
Could the Moon serve as a giant gravitational wave detector and provide new confirmation of Einstein's General Relativity?
In this thesis, we review in detail the interaction between gravitational waves
(GWs) and the Moon, treated as an elastic body, as presented in a paper by
M. Kachelriess and M. P. Nødtvedt. The aim is, to combine the content of
this paper with additional findings from previous literature to make the topic
more accessible.
Building on the theoretical framework of elasticity, we derive and linearize
Cauchy’s equations of motion to model the Moon’s response to such a GW.
By investigating toroidal and spheroidal oscillations induced by a GW in
different polarizations, we derive the differential equation systems to predict
the Moon’s displacements, which can then be numerically solved. The results
of different papers are summarized to get the eigenfrequencies and modes of
these displacements. We furthermore provide some insights on frequency-dependent response.
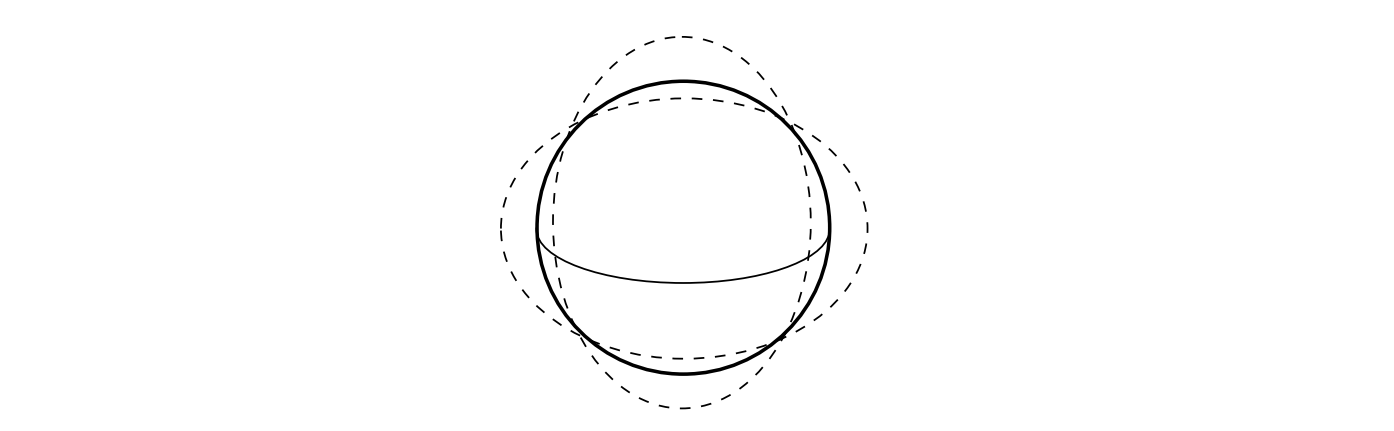
A Normal Mode oscillation of the Moon, caused by a Gravitational Wave.